Департамент образования г. Москвы

Московский институт открытого образования

Примерные задания школьного тура математической олимпиады

8 класс

1.   Числитель дроби увеличили на 5, а знаменатель – на 2 (числитель и знаменатель – целые положительные числа). При этом значение дроби уменьшилось. Приведите пример, как такое могло произойти.

2.   Дано трехзначное число ABB. Если перемножить его цифры, то получится двузначное число АС, а если перемножить цифры АС, то получится С. Найдите исходное число.

3.   Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. Когда поезд отъезжал, каждый из них насчитал еще несколько скамеек, причем один из них насчитал в три раза больше, чем другой. А сколько насчитал третий?

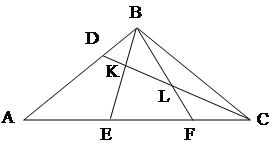
4.   В треугольнике АВС (см. рисунок) CD – биссектриса угла ACB, АВ=ВС, BD=BK, BL=CL. Докажите, что BF – биссектриса угла CBE.

5.   Имеется 6 гирь: по паре зеленых, красных и белых. В каждой паре одна гиря тяжелая, а другая – легкая, причем все легкие весят одинаково и все тяжелые весят одинаково. Можно ли определить 3 тяжелые гири за два взвешивания на чашечных весах?

6. У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1·0·0 до 9·9·9. Чему равна их сумма?

  5 класс    6 класс     7 класс     8 класс     9 класс     10 класс     11 класс