Департамент образования г. Москвы

Московский институт открытого образования

Примерные задания школьного тура математической олимпиады

11 класс

1.   Придумайте такое нецелое число, что 15% и 33% от него – целые числа.

2.   Найдите сумму: 100²–99²+98²–97²+...+2²–1² .

3.   Встретились несколько друзей. Каждый из них обменялся рукопожатием с каждым, кроме Федота Бурчеева, который, будучи не в духе, некоторым пожал руку, а некоторым – нет. Всего было сделано 197 рукопожатий. Сколько рукопожатий сделал Федот?

4.   Докажите, что для любых x и y справедливо неравенство:

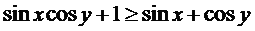
5.   В четырехугольнике АВСD углы А и С – прямые. Из точек В и D опустили перпендикуляры на диагональ АC и получили соответственно точки M и N. Докажите, что AM=CN.

6.   Существует ли одиннадцатигранник (не обязательно выпуклый), у которого каждая грань – многоугольник с четным числом сторон?

5 класс    6 класс     7 класс     8 класс     9 класс     10 класс     11 класс