Департамент образования г. Москвы

Московский институт открытого образования

Примерные задания школьного тура математической олимпиады

10 класс

1.   Придумайте такое нецелое число, что 15% и 33% от него – целые числа.

2.   Найдите сумму: 100²–99²+98²–97²+...+2²–1² .

3.   Встретились несколько друзей. Каждый из них обменялся рукопожатием с каждым, кроме Федота Бурчеева, который, будучи не в духе, некоторым пожал руку, а некоторым – нет. Всего было сделано 197 рукопожатий. Сколько рукопожатий сделал Федот?

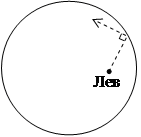
4.   На круглой арене цирка (но не в ее центре) стоит тумба, на которой сидит лев. По команде укротителя лев спрыгивает с тумбы и бежит по прямой. Добежав до бортика, он поворачивает на 90⁰, снова добегает до бортика, поворачивает на 90⁰ и т.д. Докажите, что на арене (но не на тумбе) можно положить кусочек мяса так, что, независимо от первоначального направления движения, лев съест мясо. (Лев съедает мясо, если его путь проходит через точку, в которой оно лежит.)

5.  У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1·0·0 до 9·9·9. Чему равна их сумма?

6.   Был квадратный трехчлен x²+10x+12. За один ход разрешается менять на  единицу свободный член или коэффициент при x. После нескольких таких операций получили трехчлен x²+12x+10. Докажите, что в некоторый момент был трехчлен с целым корнем.

5 класс    6 класс     7 класс     8 класс     9 класс     10 класс     11 класс